행렬 0x02: 선형사상(작성중)

원문: Ecole 42, matrix subject. “Enter the Matrix, An introduction to Linear Algebra” by Tristan Duquesne, Luc Lenôtre. 1.2ver

선형 사상

$V$와 $W$를 같은 체 체 $K$ 위의 두 벡터 공간이라고 하자. 그리고 $u,v ∈ V$를 두 벡터, $𝜆 ∈ 𝐾$를 스칼라라고 하자.

함수 $f : V → W$가 선형 사상이라고 불리기 위한 조건은 다음과 같다.

1. $∀(u,v) ∈ V^2$, $f(u + v) = f(u) + f(v)$
2. $∀λ ∈ K$, $∀u ∈ V$, $f(λu) = λf(u)$

이 속성들이 확인되면, $f$가 벡터 공간 $V$에서 새로운 벡터 공간 $W$로 값을 선형적으로 사상(mapping)한다고 한다. 기하학적으로 선형적이라는 것은 입력 공간에서 평행한 두 직선이 변환 후에도 평행하게 유지된다는 것을 의미한다.

이 조건들은 필요충분 조건이다. $f$가 선형임을 증명하려면 위의 두 방정식이 참임을 증명해야한다. 두번째 방정식은 입력공간 $V$의 영벡터 $0_V$가 출력 공간 $W$의 영벡터 $0_W$로 사상된다는 것을 의미한다.

다음 다이어그렘을 통해서도 상황을 이해할 수 있다.

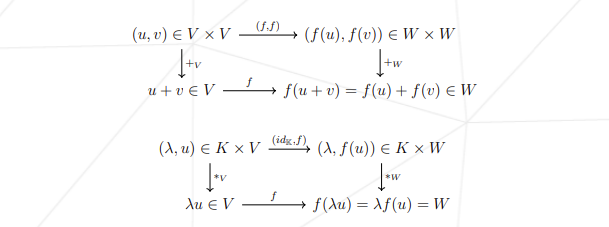
더 간결한 형태는 다음과 같다.

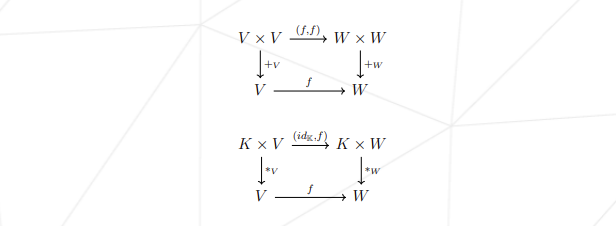
이 가환(순서가 바뀌어도 결과가 동일한) 다이어그램이 참일 때, 시작점에서 끝점까지 어떤 경로를 택하든 동일한 결과에 도달한다는 것을 의미한다. 먼저 $f$를 적용하거나 벡터 공간 연산자를 사용하는 선택은 중요하지 않다. 단 연산이 이어지기만 하면 된다. 잠시 멈추고 다이어그램들이 위에 쓰여진 선형성 방정식과 어떻게 동일한지 이해해보면 좋다.

보통 선형대수학에서 선형사상 $f$는 행렬에 대응된다. 정확히 말하면, $V$가 $n$차원이고, $W$가 $m$차원이며, $V$와 $W$가 각각 기저를 제공받는다면, $f$는 $𝑛 × 𝑚$행렬, 즉 $n$개의 행과 $m$개의 열을 가진 행렬로 고유하게 표현될 수 있다.

작성중